regression 回归
linear model 线性模型
1、设计模型
2、评价确定的参数是否合适，利用Loss function L，损失来评价
3、通过数据训练模型training data
4、testing data计算ERROR
挑选最好的function，也就是使得损失最小的function
计算方法：梯度下降Gradient Descent，寻找L（loss）的最低点
- 随机选取初始点W0
- 计算W0对L的微分，切线斜率，判断w0的值如何变动（取决于微分与learning rate），w0-》w1
- 反复执行第二步
- 最后找出的是局部最优解，也就是微分为0的位置。不一定全局最优（linear上不存在这个问题。没有局部最优解）
- 关于推广：一个参数推广到两个参数的时候，也就是偏微分的计算，与一个变量原理相同。
5、优化模型：再设计、再训练、再评价，模型由简单到复杂
model越来越复杂，training data 越来越匹配，但testing data表现不一定 ——》overfitting 过拟合，所以要选择合适的model
适当引入feature用于分类（？），可以使模型更匹配
Q:为什么我们更期待一个参数更接近0的function?
A:比较平滑的，参数小可以让输入对于输出的变化不敏感。（？）
1、bias的影响：看结果集合与中心的偏离程度 （模型的复杂程度影响，越复杂，bias越小）
样本均值和总体均值的关系（？）———无偏估计
样本均值的期望等于总体均值———bias小
2、variance的影响：看结果集的分散程度（模型的复杂程度会影响variance,越复杂，variance越大)
样本方差和总体方差的关系（？）———有偏估计
简单model受到样本数据的影响比较小
确定一种model，相当于确定了一种范围，模型越复杂，范围越大，范围越大。点更容易分散
两者越低越好，寻找平衡
variance大：overfitting（training拟合好，但是test拟合不好）————增加data/regularization正则化
bias大：underfitting（training拟合不好）————重新设计model
更复杂：更多的feature，更高的阶层
Gradient Descent 梯度下降
过程：
其中
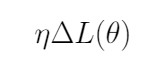即为梯度，因为前面有了负号，所以点的移动总是向着梯度下降的方向进行，因而叫做梯度下降。关于learning rate
太小：梯度下降处理速度慢
太大：直接错过min值
措施：关注前几次的参数updates，画图(如下图所示），可以提前发现太大的learning rate，当loss值可以稳定下降的时候，rate才相对合适
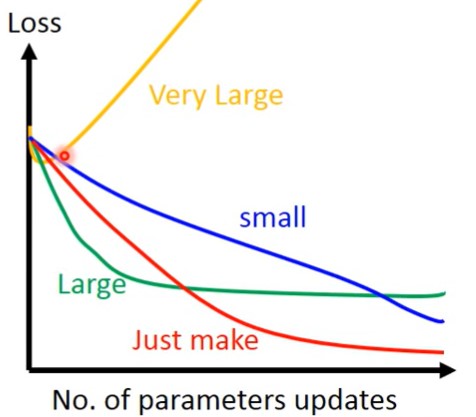
调整方法：可以将learning rate 成为t（次数）的函数。learning rate的变化规律一般为：值可以先很大，方便我们快速定位到最小值附近，然后值减小，慢慢靠近最低值，防止因为值过大错过最低值。
注意！learning rate也是要随着不同的参数而变化的，不是一成不变的，而且对于同一时间段的多种参数（如w，b等），learning rate 依旧有差别
Adagrad：
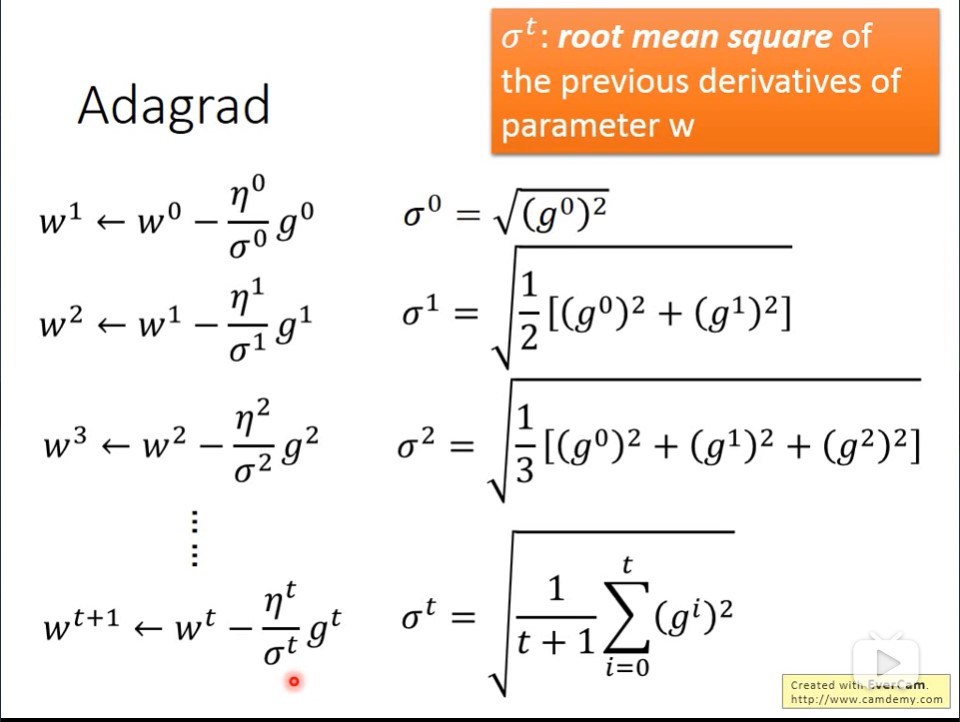
g是对应参数关于x的微分或偏微分，所以η是关于下降次数(t)的函数，σ是关于对应参数微分(g)的函数，由此得出的learning rate可以和t与g相关
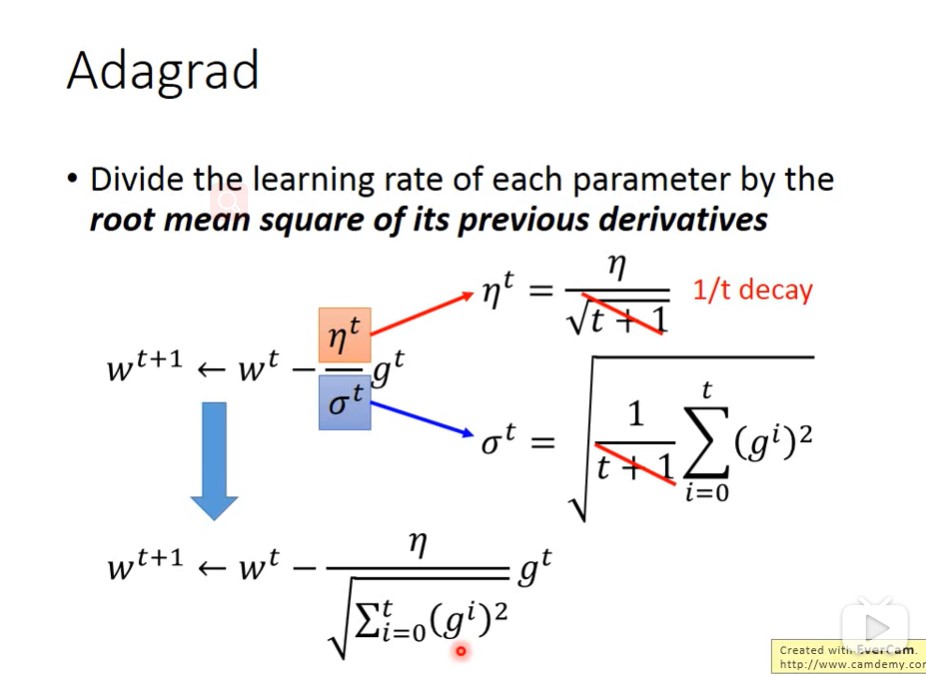
Stochastic
只选择某一个example的Loss值，通过一个example进行梯度下降，得到相应参数。
- 好处：速度快，同样的起始点，可以update参数的次数变多了，计算内容少，更快。
Feature Scaling 特征缩放
让不同的特征，有相同的比例，统一到一定的范围内。让每个参数对目标的影响程度相似。这样子learning rate也能够相对平稳一些。
方法：
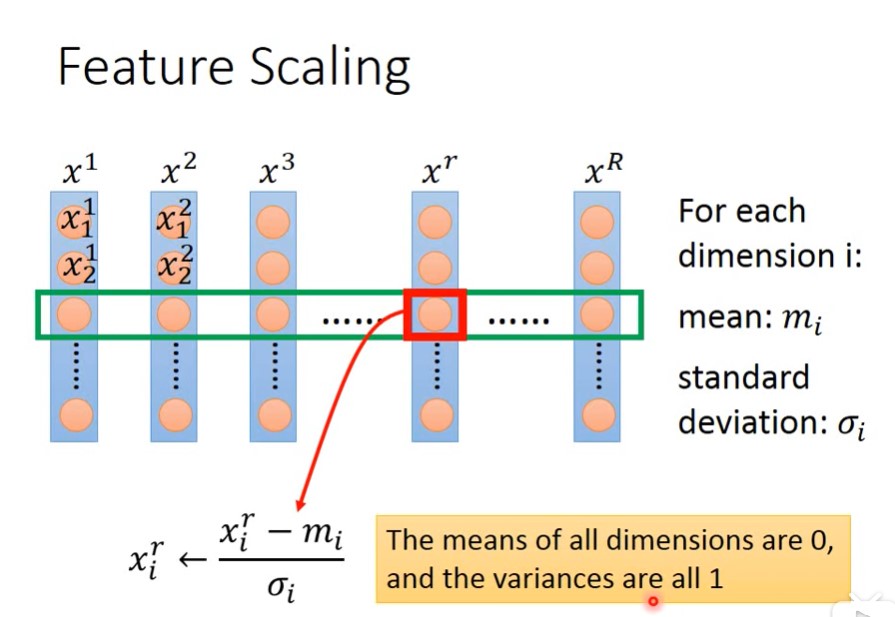
mean：均值，standard deviation：标准差
Theory 理论基础
泰勒级数，泰勒展开
