Classification 分类
1、理论方法:三步走

概率知识:贝叶斯公式(后验概率),高斯分布
伯努利分布 == 二项分布
高斯分布 == 正态分布
一般过程
假设一个机率模型
1、training data 估测一个gaussian distribution(高斯分布结果),通过高斯分布计算出新的x在范围内被选择出来的几率。
2、不同的高斯分布对应不同的likelihood(可能性),找到分布中,面对training data数据,标记概率(likelihood)是最大的,选择这样的分布,得到相应的参数。

穷举各种μ与ξ的值,然后通过图片方法计算,选择最大可能性的一组参数
3、每个class都要计算第二步,得到相应的(μ,ξ)。
4、分类计算,计算输入的x来自于不同的class的几率

5、效果不好的时候(比如二维空间分类分不出来),可以提高feature的维度,即增加输入向量的长度。(最后计算效果不好!!:triumph:)
改良处理
1、减少模型参数,参数越多越容易overfitting,让不同的class共用一个ξ,使得likelihood最大。
计算参数方式:μ的计算同上,ξ的计算不同,需要加权计算一下,likelihood函数也不同,如图下

相同的ξ,让boundary变成了直线,这也是linear model。
计算后得出准确率高了很多。
阶段总结——概率模型做(二)分类

相关数学知识(扩展)
1、linear model的导出过程:
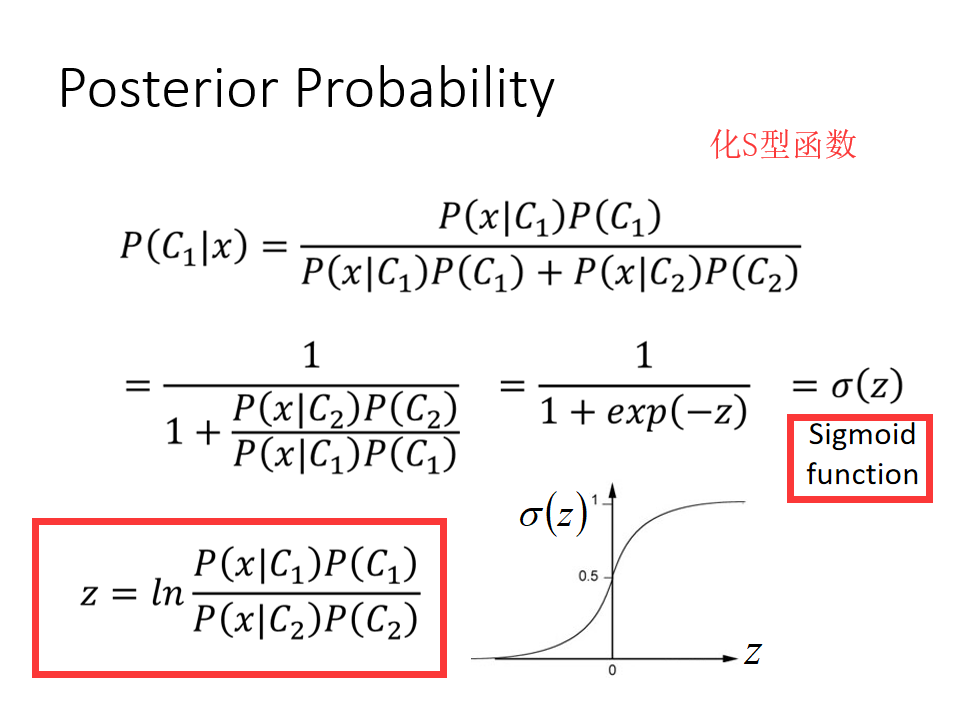


logistic Regression
回顾分类设定的模型:
这是一个逻辑回归函数
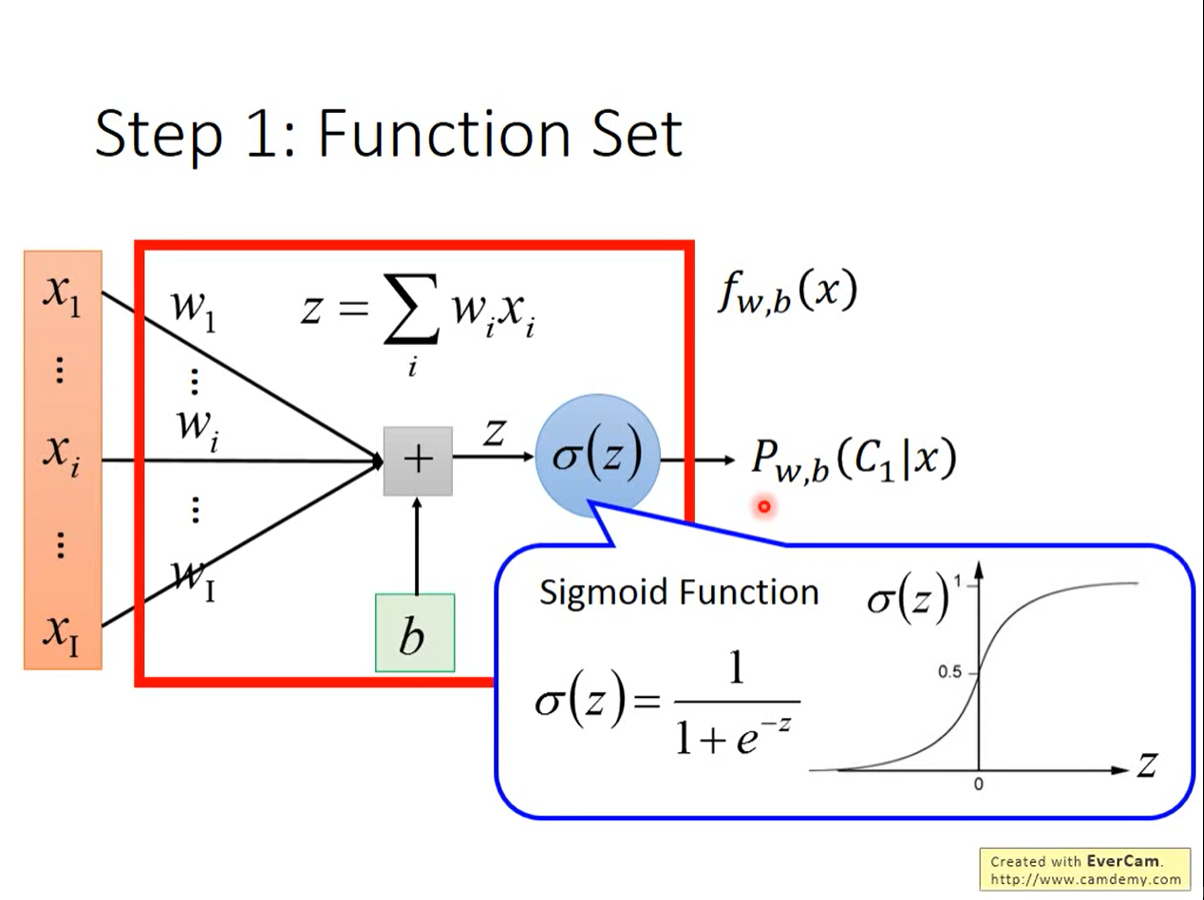
2、通过训练集,选择出最合适的w,b参数:定义function的好坏

L是发生训练集所展现分类的概率函数,假设每个元素属于某一类都是相互独立的,所以计算L的方式是将计算出的概率(f函数)相乘。让L最大值所对应的w,b的值,就是我们模型中需要找出的w,b的值。
++++++++++++++++++++
下面是数学相关的L函数的化简整理
理解这几条:
因为L是累乘的结果,为了方便计算,取ln变成累加,再整体取符号,化取最大值为取最小值。
引入y^,(二分类中)y取1表示输入class1,取0表示属于class2.
将每一项的形式都通过y^的引入而同一成相同形式
统一出来的相同形式是两个二项分布的交叉熵,其中交叉熵越接近0代表两个分布越相同,我们想要的就是交叉熵尽可能接近0.
以下是ppt讲义部分:


其中y的取值只有1与0,f因为是个概率函数取值在0-1之间,所以方括号内的部分一定是小于零的,加上外面的负号会大于0,所以方括号越趋近于零,一个是代表两个分布越接近,另一个也是代表-lnL的值趋向最小,表示模型越来越匹配,所以交叉熵越趋近于0越好。
下面的H是交叉熵的计算方法。
于是我们可以得到逻辑回归(二分类)的判定模型好坏的函数L。
逻辑回归与线性回归的对比

Q:为什么不能直接使用线性回归的L函数(square error)当作逻辑回归的L函数,线性的相对而言更简单易算?
A:利用梯度下降的方式逼近最合适的w的时候,会出现无法区别距离实际值到底很近还是很远的状况,在梯度下降的时候会卡住,不容易得到好的结果:
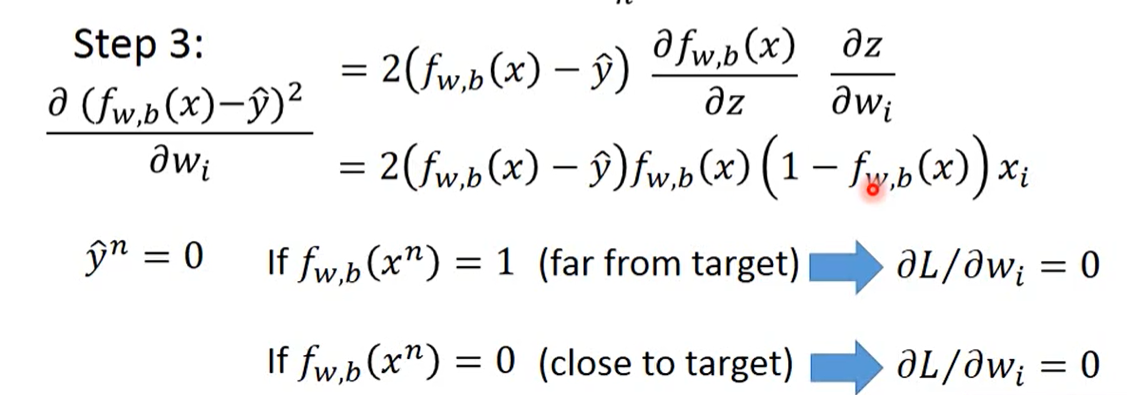
3、通过Loss函数计算最佳w,b的方法:
数学问题,对Loss函数对w求偏微分,通过一系列变换,得到一个直观的结果。然后通过梯度下降的方法,求得loss的最低点w的值
总结对比

生成模型和判别模型对比(有些不懂)
(暂时理解)生成模型是最初的分类模型,计算ξ、μ参数的那个模型(假定过分布服从正态分布)
判别模型就是上面的概率模型,直接计算w,b参数的模型。
两个模型实质是相同的,(w,b),(μ,ξ)也都有一定对应关系,但是计算出的结果会发现参数的结果不同,也就是求出的具体模型是不同的。原因就在于生成模型提前有过很多假设,也对模型的计算产生一定的影响。
生成模型(generative model)的好处是:
- training data很少的时候,生成模型受data的影响小,有自己的假设,有时反而表现很好
- data可能本来存在问题的时候,因为受data影响小,所以可能表现更好。
判别模型的好处是:
- 受data影响大,所以数据足够多足够准确的时候,计算出来的模型更优。
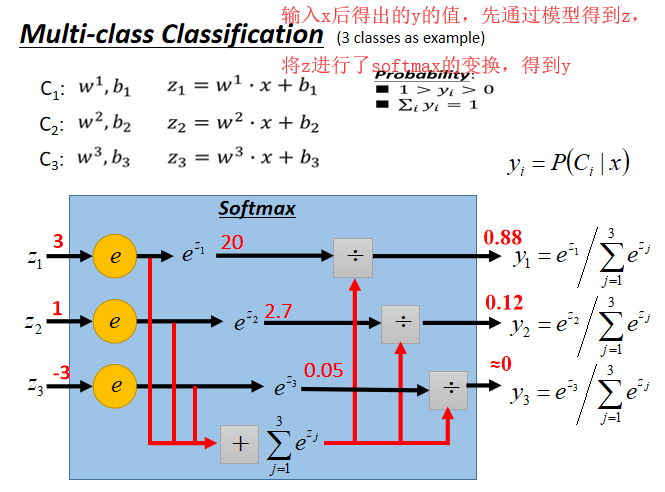
多分类问题(三分类为例)
(笔记记得稍微有点简单,先大体理解一下)
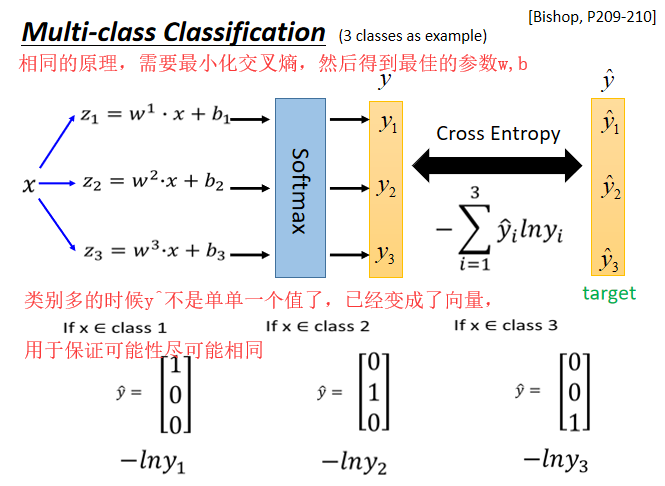
逻辑回归的限制
因为回归依旧是一条直线,所以总会存在,根本无法通过一条直线将类别分离的情况。
解决方式:Feature Transformation
将特征值转化
eg: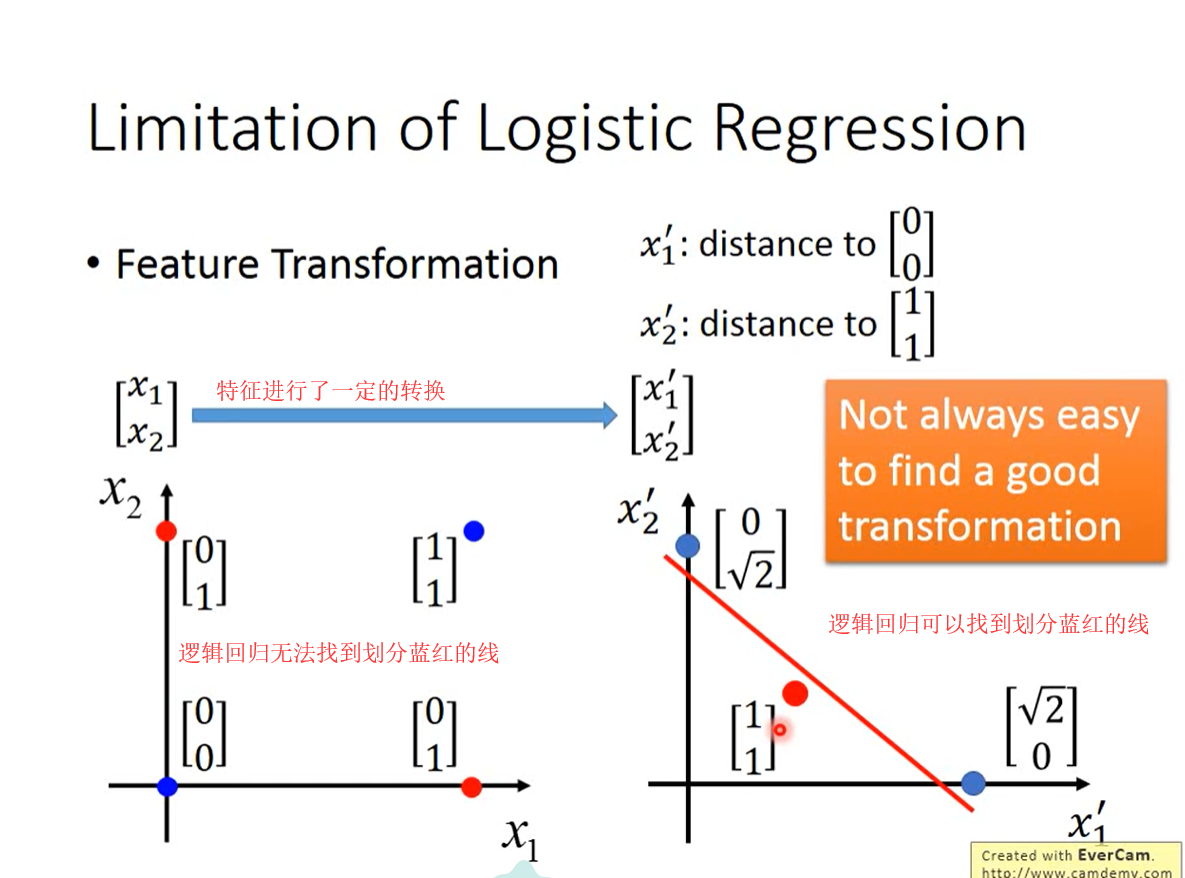
问题:如果找到合适的transformation?
回答:交给机器
进行多层的logistic regression,直到类别可以完全分开。然后将处理好的新的特征值,再进行逻辑回归,得到好的模型结果。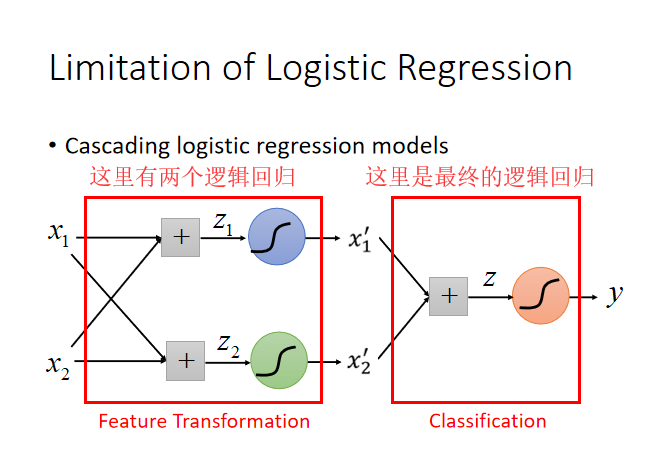
每一个逻辑回归又叫做“神经元”(neuron),整个网络是神经网络(neural network)


