Backpropagation——反向传播
是有效计算gradient的向量的方法,因为随着网络的层数的增加,参数越来越多,向量越来越长,计算越来越复杂,使用反向传播比较高效。
预备知识
chain rule 链式法则
用于多变量求导

σ(z)函数

backpopagation过程
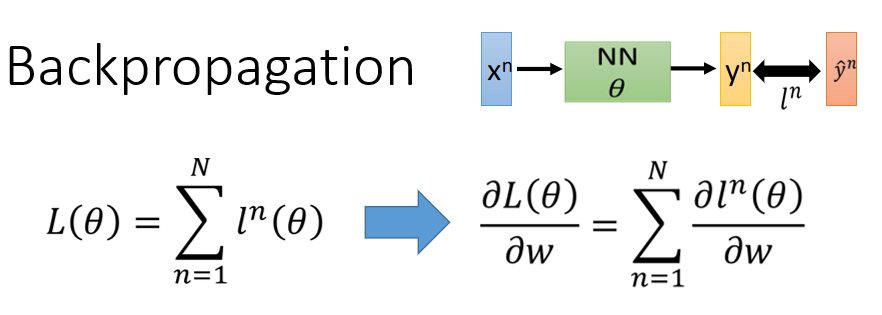
梯度下降的方式是用于求得Loss函数的最小值,loss函数是一个求和函数,取决于每一个l的值,所以重点在于计算w参数对C的微分。
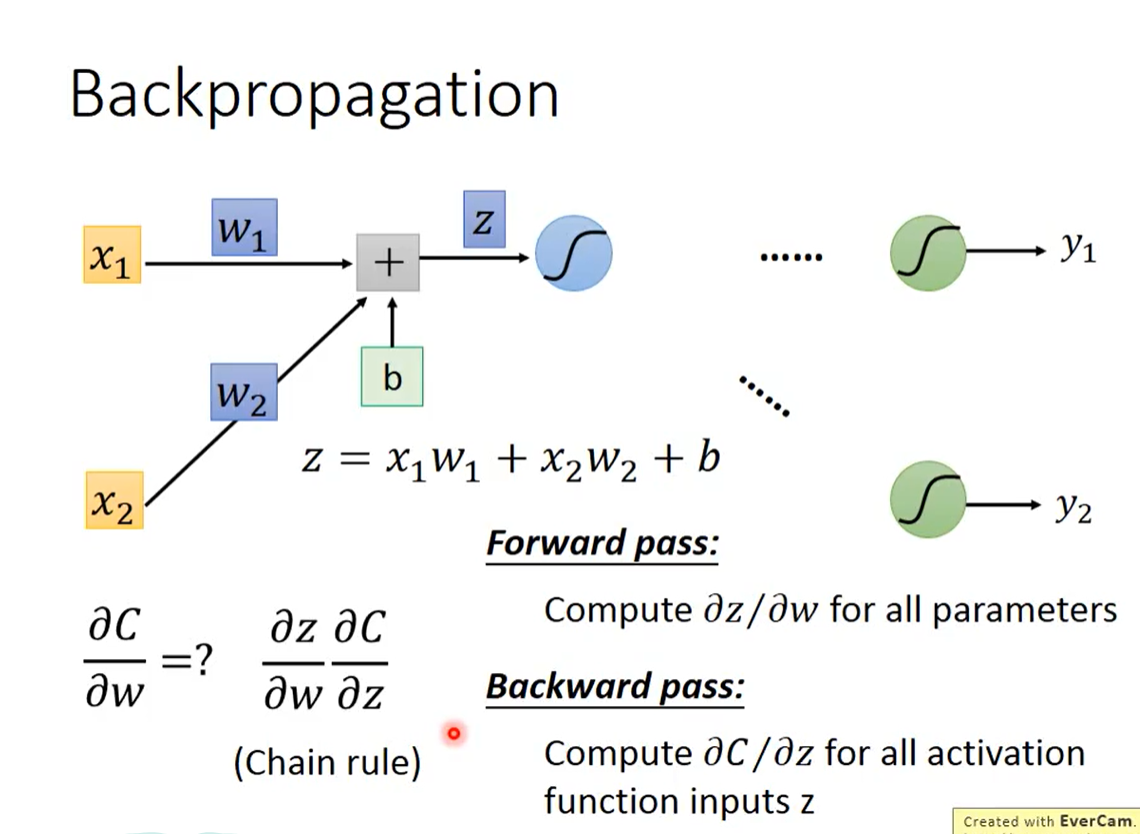
(其中C就是上图的小l)
求w对C的微分,可以通过链式法则分解,引入中间变量z。
求w对z的微分是forward pass,有图可得,w1对z的偏微分就是x1,可以以此类推,wn对z的偏微分,就是wn前面的input值。
求z对C的微分是backward pass
Forward pass
正如前面所述,wn对z的偏微分,就是wn前面的input值。一定是当层的、最接近的input的值,可以是来自外部输出,也可以是来自前一层网络。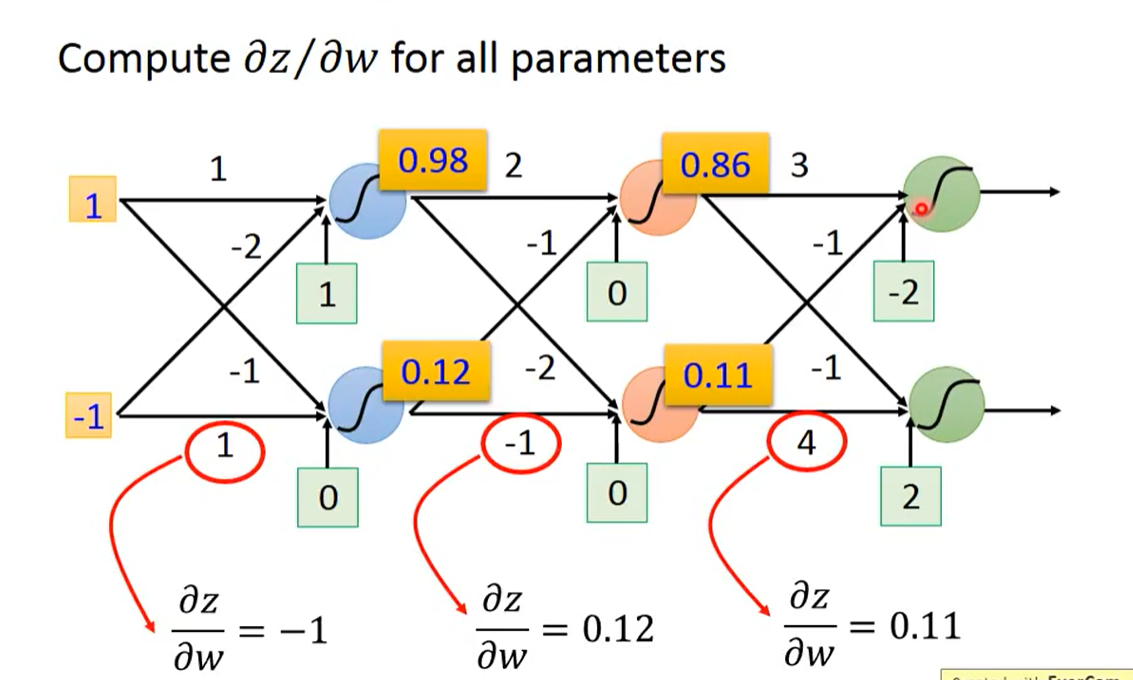
Backward pass
考虑的是下一步发生了什么事情。
引入中间变量a,使得a = σ(z)
可以通过链式法则展开,得到z对C的偏微分。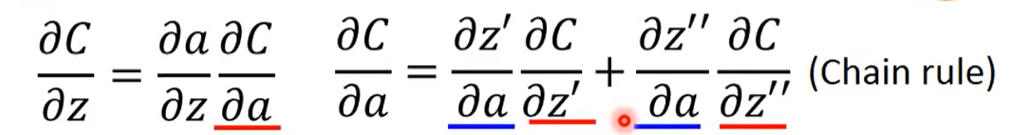
其中可以看到关系可以普遍简化定义为:a会影响z’,z’’(可能还有别的z),z’,z’’会影响c,从而有a影响了c,通过链式法则可以表示出c对a的偏微分。
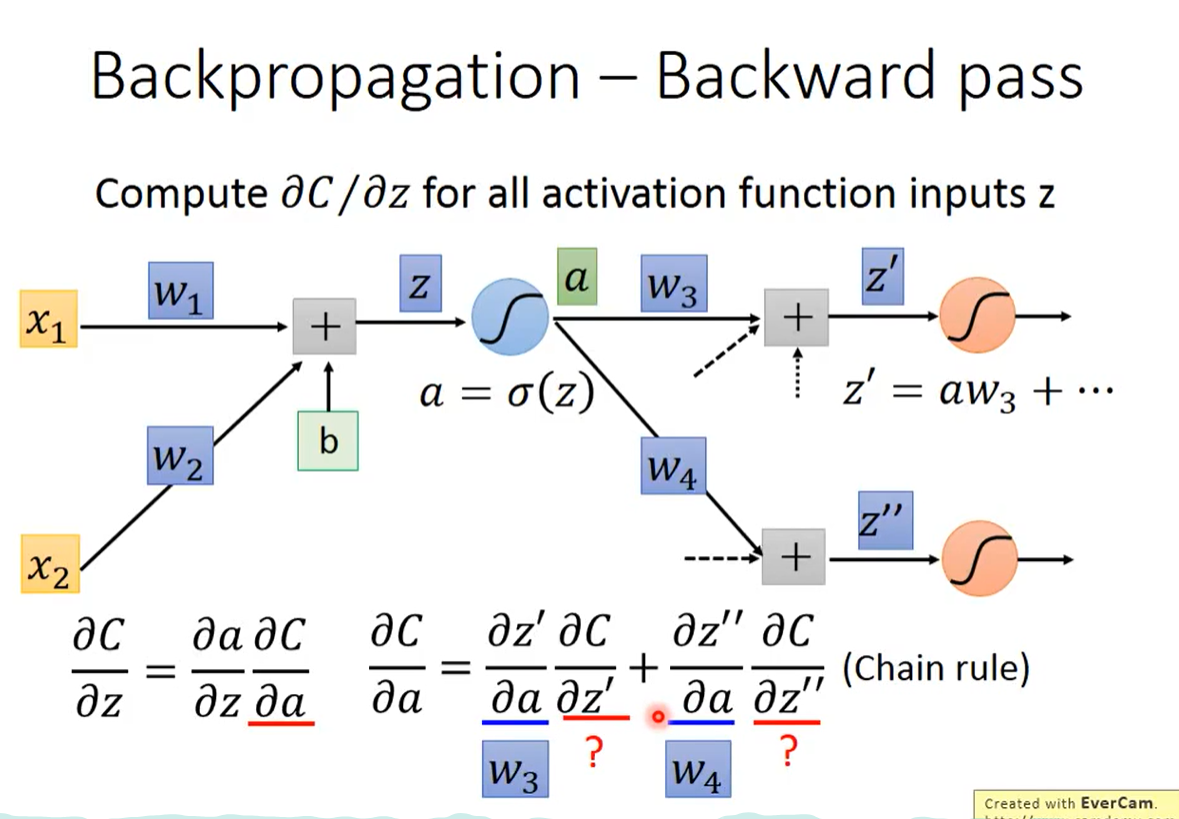
第一项a对z’等的偏微分都很好算,a是作为input的层,通过forward pass可以知道,对应的是w1,w2……wn,后面那一项我们无从下手。
假定我们已经知道后面那一项的值,则整个式子可以进行一定的整理
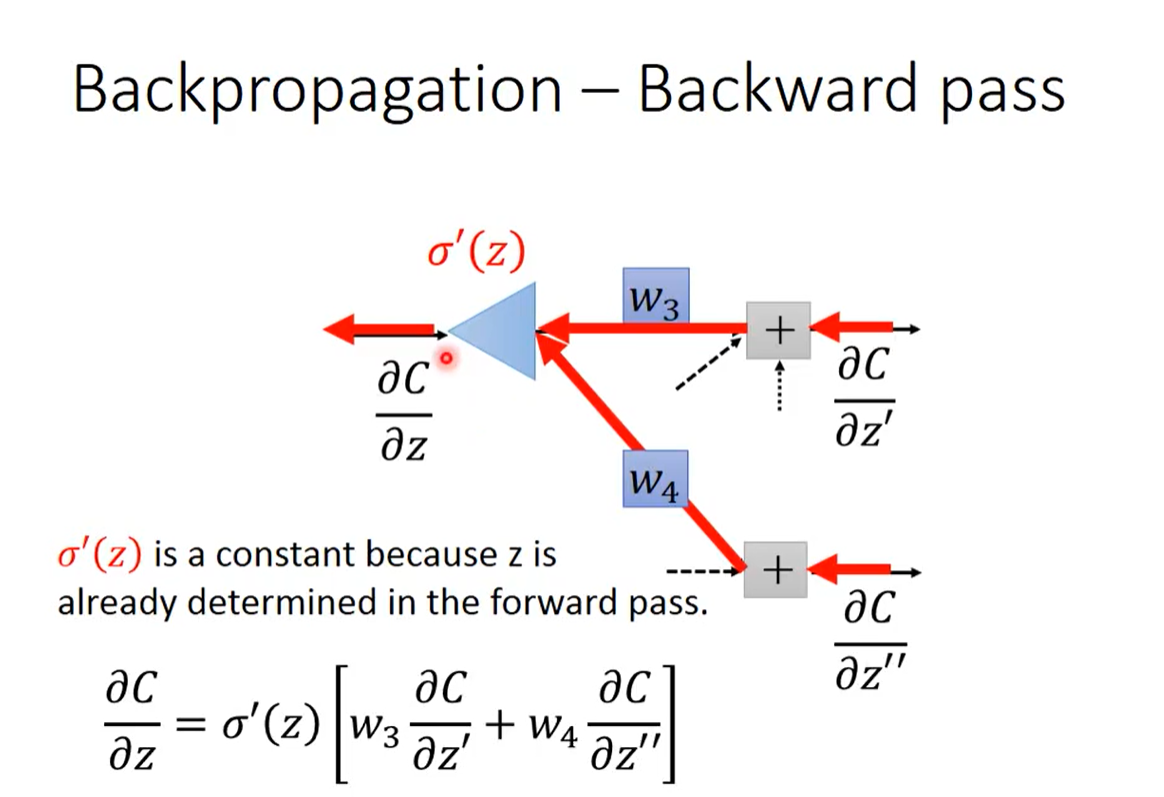
如何计算未知的两项? – 分类讨论
case 1:已经到达了output layer
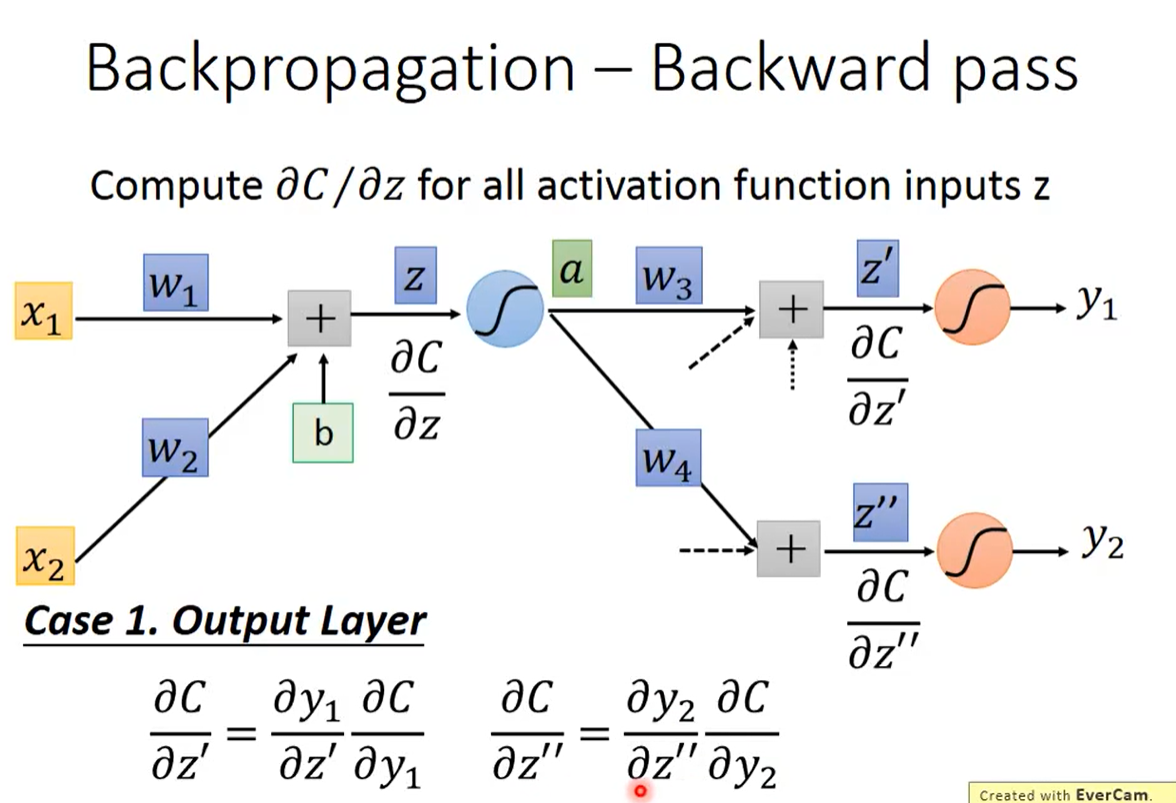
case 2 Not output layer
通过递归的方式计算,直到打倒了output 层,然后可以回溯到前面层
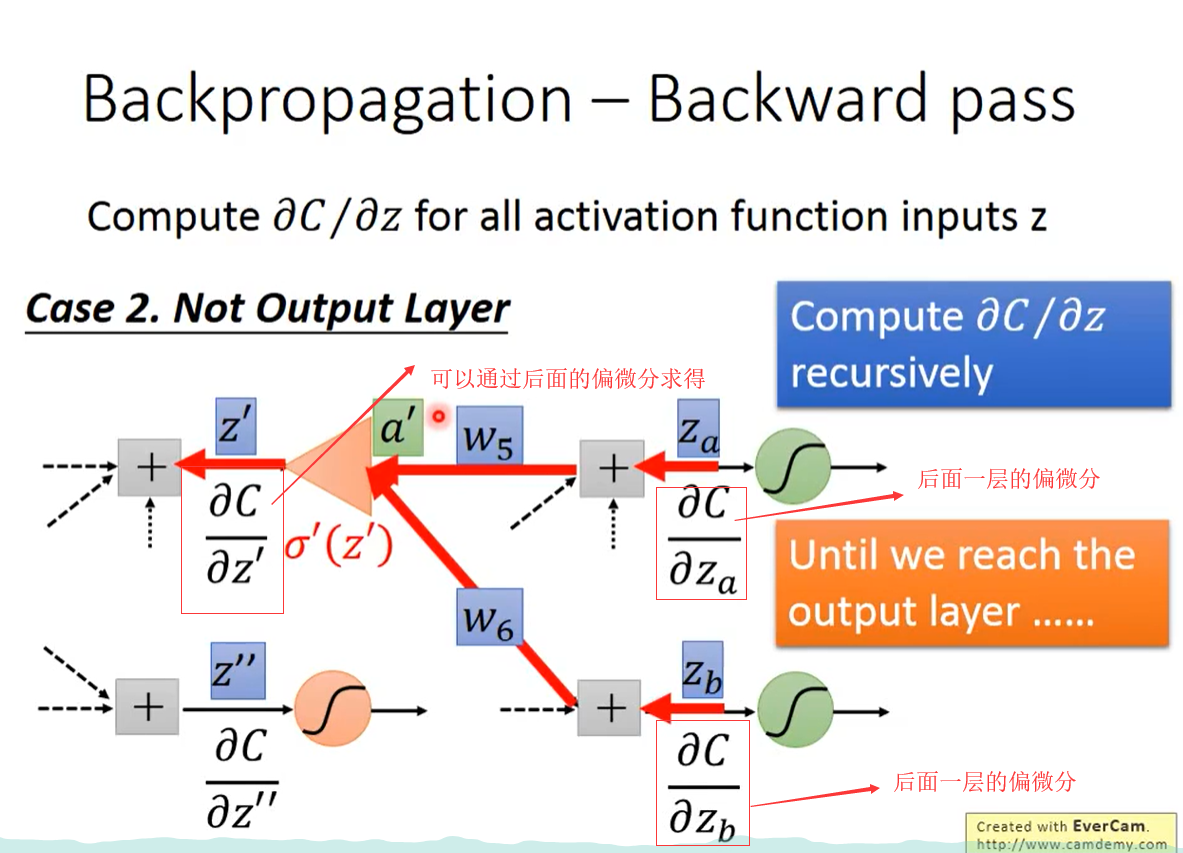
实际计算方式
computer z对c的偏微分 from the output layer,从输出层向后计算,计算有效率。
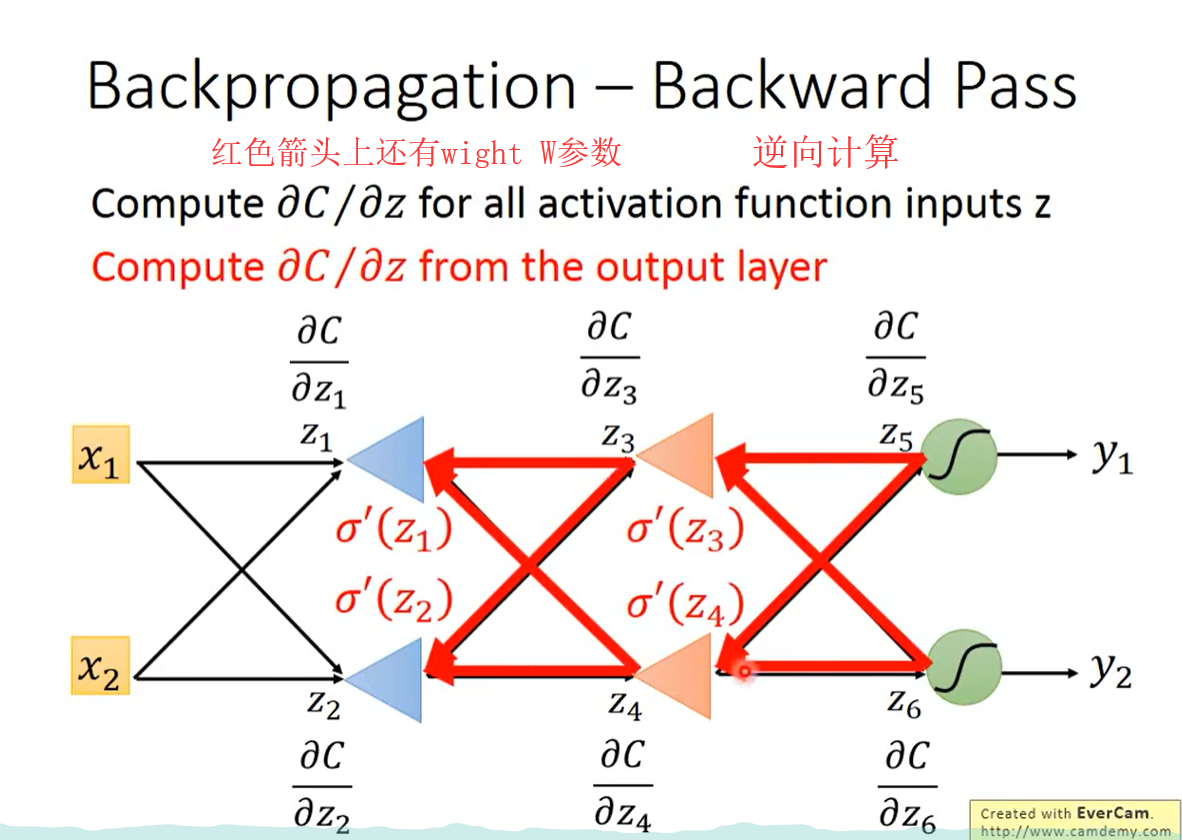
实际是,建立一个反向的神经网络,来计算整个的偏微分。
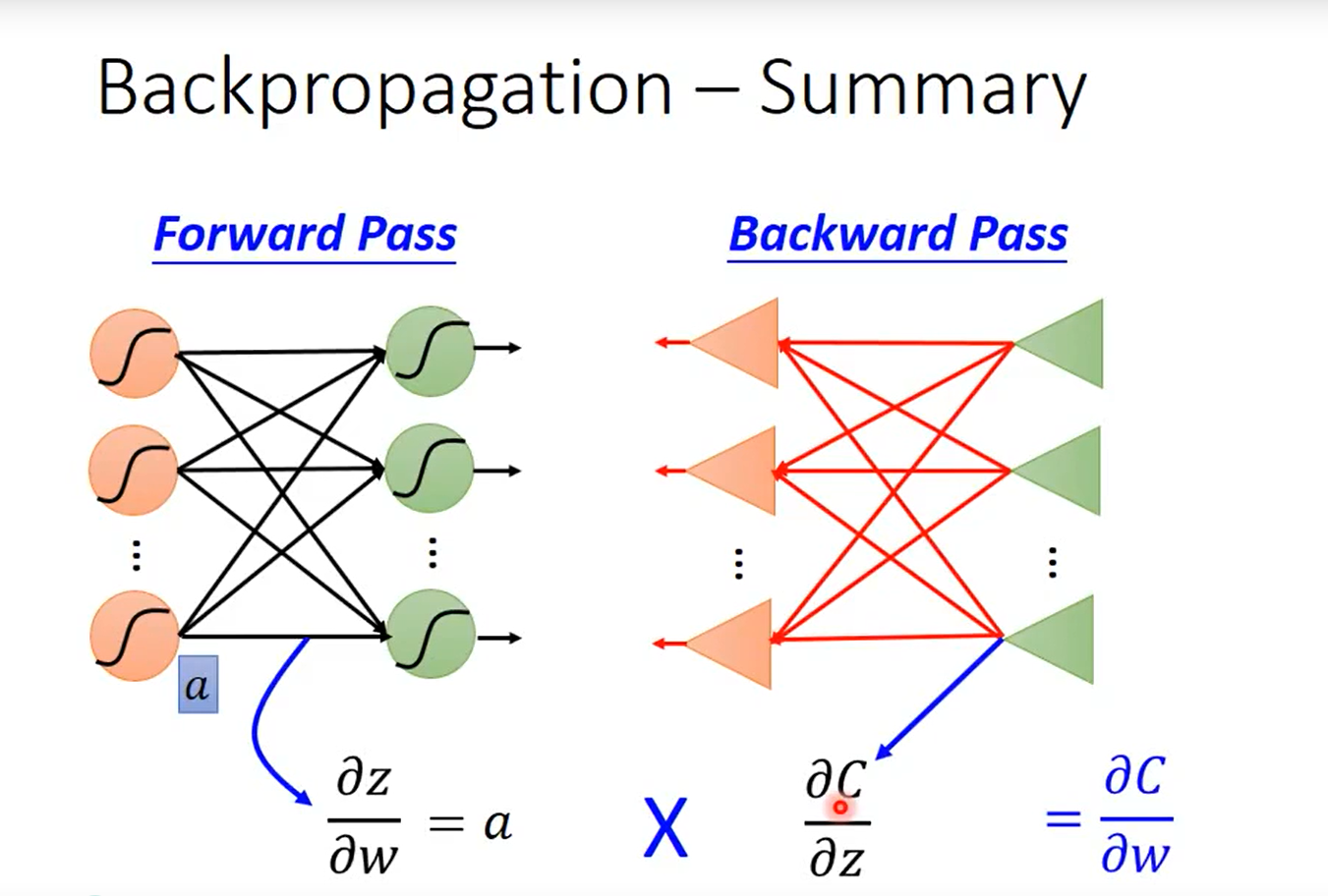
Summary
- 先计算ForWard pass
- 再通过逆向网络计算 Backward pass
- 两者相乘,最终得到了w对C的偏微分