Structured support vector machine

Separable(应用范围较窄)
使用structured Perceptron 结构化感知机

问题:
这个算法什么时候才能够收敛,可能成功的找到需要的W吗?
结论:
算法花费最多的次数是(R/margin)的平方次

Non-separable case
我们大多数时候可能找不到可以让正确的(x,y)对的值最大的W向量,但是我们依旧可以评价不同的W向量的好坏。
为了评价W向量的好坏–>定义Cost Function,用来评估W有多差,然后我们选择的W是使得Cost Function minimize的。
Cost Function可以根据不同的问题自己定义。
Cost Function的最小值的求解可以通过梯度下降的方法。
特别地,当learning rate = 1的时候,这个就变成了结构化感知机。
Considering error
不同的错误之间有差别,这个也应该考虑到Training中来。
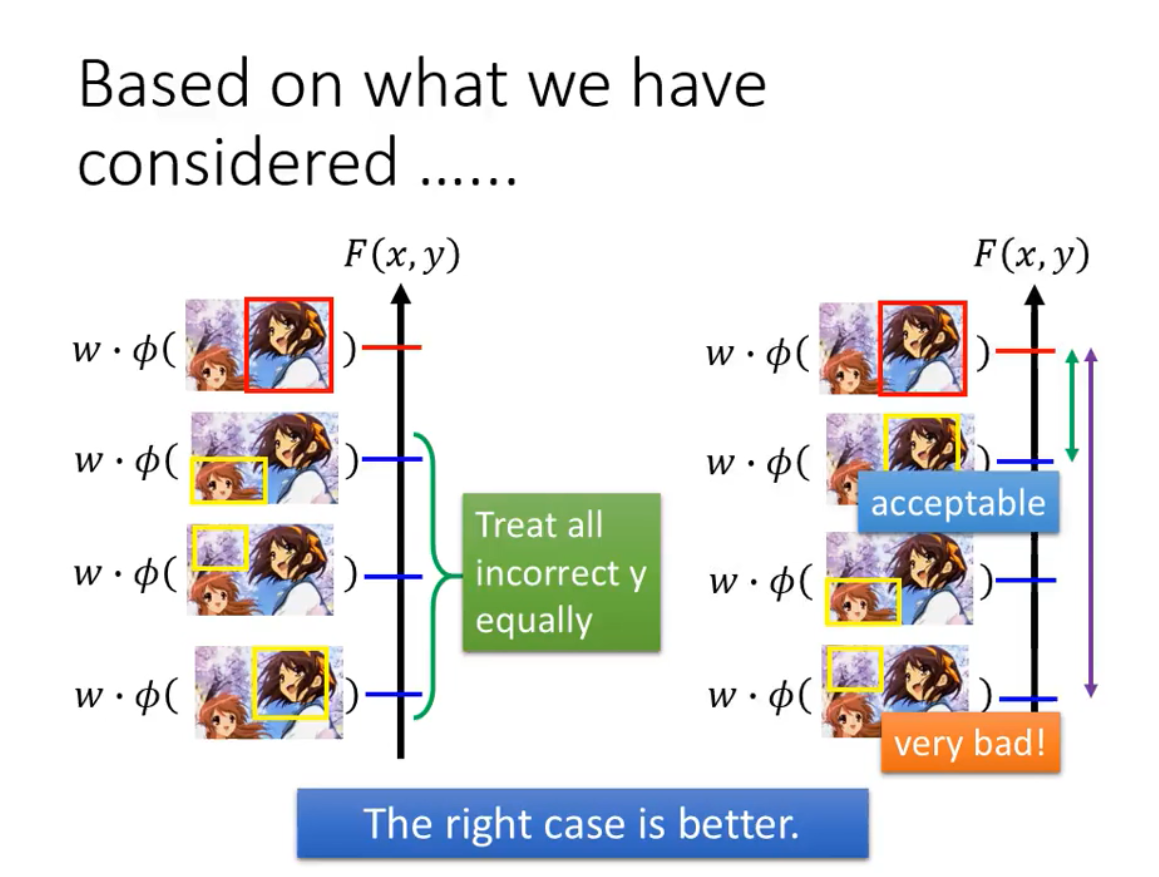
如图所示,右边对应的W就比左边对应的W要好很多。
所谓考虑错误的差别,即我们希望找到的W对应的评测函数F,当虽然是错误但是和正确答案比较接近的时候,两者的评测值也是接近的。但是当错误很离谱的时候,评测值和正确的评测值之间的差距则相对大了很多。
做法:定义Error Function,这个函数也是自己根据不同的问题自主定义。
有了Error Function,对应的Cost Function也需要作出相应修改,表示错误的差别被考虑进了training当中。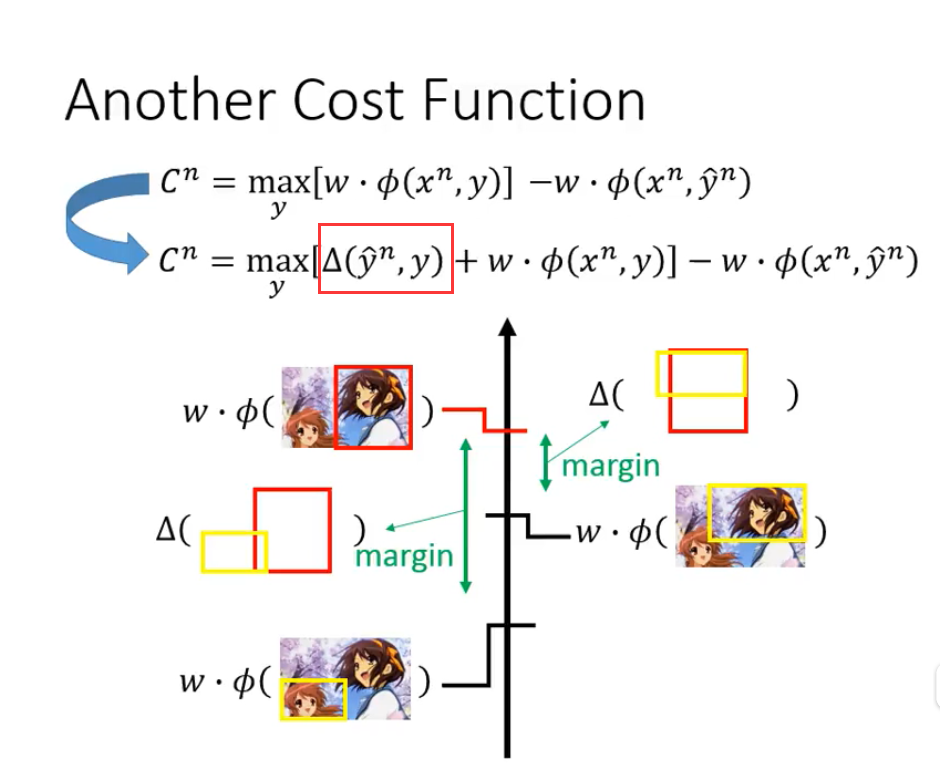
(存疑?为什么最大值是要加上Error Function)
计算Cost Function同样使用梯度下降
注意:此时出现了一个问题,最大值的求解对象是改变了的,原本只是求W*Feature的最大值,这个是我们假定已经能解决出来的,现在需要求出来的是原来的值加上Error Function的值。这点提示我们Error Function要合理定义,便于计算,不然会给整个计算增添很多问题。

算是一种理解方式?当式子满足下面两个的时候,上面的不等式是成立的,上面的不等式成立了,我们才能通过不断地减小真实y值和使F值最大的y值之间的最大差距来减小实际差距。
Regularization



