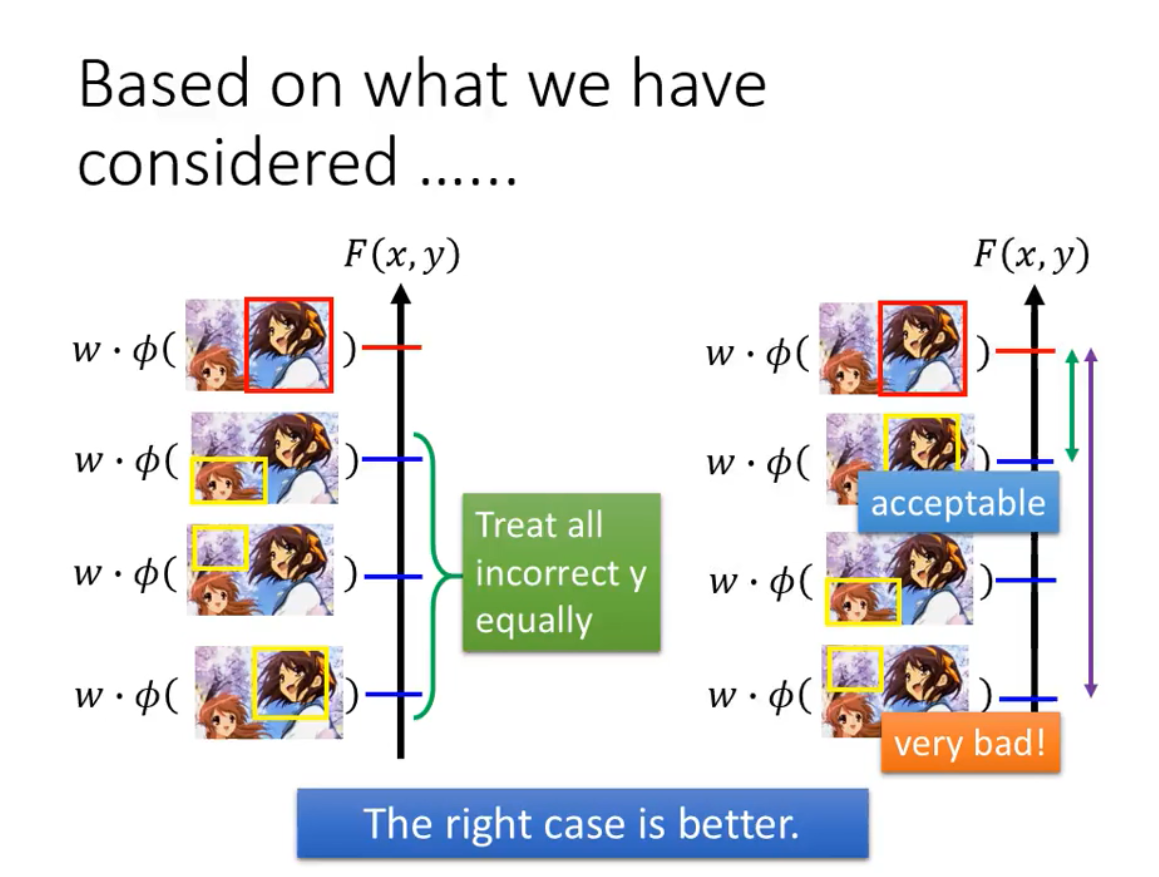
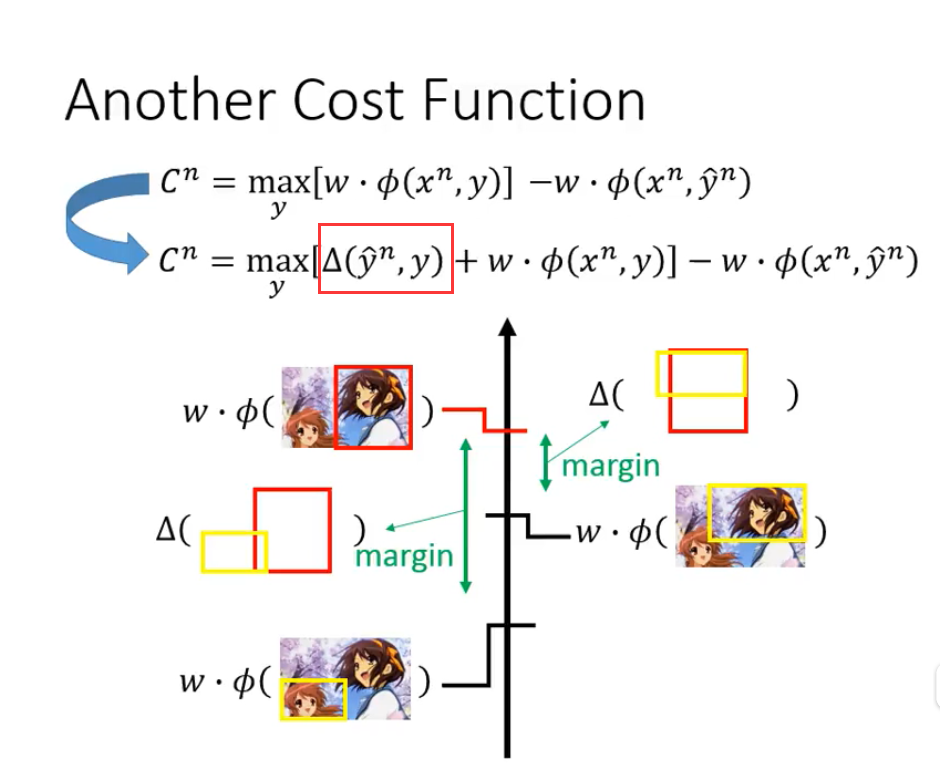
Sequence Labeling Problem
以下都是以POS问题(词性标注问题)为例
HMM(隐马尔科夫模型)
假设:
产生句子分为两个步骤:
- 产生一个POS的序列,基于大脑中的语法。
- 根据POS序列的tag,找到对应词性的单词,对应方式是基于词典
- ->形成一句话
概况
Step 1: 根据马尔科夫链,计算产生相应POS的几率
step 2:基于相应的pos序列,在指定位置上配上某一单词的几率,将整句话组成的序列相乘,也就得到了在该pos序列条件下,生成这句话的几率。
基于以上两个步骤,利用条件概率公式,可以计算出X:句子序列,Y:词性序列,两者相匹配的几率。下图是一个例子:
更一般化的描述:
其中的各种几率根据training data可以统计得到
计算方式
已知x,想要求的Y,实际上就是通过穷举所有的Y,找到让P(x,y)最大的Y的过程。
直接通过暴力枚举的话算法的复杂的非常大,借助viterbi algorithm可以将复杂度大幅度降低,提高效率(一般复杂度为O(L|S|2),L为序列长度,S为词性元素)
Summary
根据结构化学习的方式,HMM解决了对应的三个问题。
存在的问题
HMM“脑补”问题:
由于HMM假设了Transition probability 和 Emission probability之间是相互独立的,得到的计算公式P(x,y)体现了这一点,两个可能性单独通过训练集进行训练。所以可能会出现HMM根据公式自主创造新序列的可能性。
这个问题有好有坏:
- 不好的地方:正确的序列的P(x,y)值可能反而小于错误的P(x,y)值
- 好的地方:当数据集数据很少的时候,通过脑补反而会有比较好的表现
CRF 条件随机场
- P(x,y)是与一个 exp(W*feature(x,y))正相关的
- HMM与CRF的本质是一样的
HMM到CRF的转换
将p(x,y)取log值,化乘为加

所有形如下图左边的求和表达式条件概率,都可以表示成右边的形式

HMM的P(x,y)表达式取log值后,可以划分为四个部分:
- 词性Y1作为句子开头的概率的log值
- 词性yi+1在yi后面出现的概率的log值(由1-(L-1)求和)
- 词性yL在句子末尾的概率的log值
- 实际单词xi对应词性yi的概率的log值(由1-L求和)

最后的结果,可以表示成两个向量做内积,其中紫色部分为w,红色部分为feature(x,y)。

w中的每一维是可以和相应的概率进行对应,但是由于不能保证W最后结果的每一维都小于1,而概率不能大于1,所以以正相关描述两者关系。
Feature vector的组成
- part1:tags和words之间的关系
类似于一个邻接矩阵,矩阵形成所有的(tag,word)对,记录的值是该对在句子中出现的次数。 - part2:tag与tag之间的关系(tag:词性+start+end组成的集合)
同样类似于邻接矩阵,所有的(tag,tag)对一一配对,形成矩阵。(tag1,tag2)指的是tag2出现在tag1之后的情况。还是记录次数。 - 其实feature(x,y)可以自己定义。
Training

如图所示
正如一般的结构化学习,在训练CRF的时候,我们希望可以定义一个函数,这里是O(w),找到的W,是可以在数据是正确的(x,y)对时,另这个O(w)最大化的函数。
在这里,我们用条件概率p(y|x)用来组成O(w)。
而组成的O(w)根据统计学公式,我们又可以写成相减的两部分。第一部分对我们而言是可见的(橙色的),我们需要最大化的;第二部分对我们而言是不可见的(蓝色的),我们需要最小化。
因为这里是最大化,使用的方法不再是梯度下降,而是梯度增加。
(具体计算有些困难,暂时没有理解)
最后的梯度上升的公式
- 绿色的部分是正确的对出现的次数,意味着s,t可以被正确匹配的时候,我们应该增大W。因而是正相关。
- 黄色的部分是其余任意的对出现的概率,意味着当s,t匹配错误的时候,我们应该减小W。因而是负相关。
summary
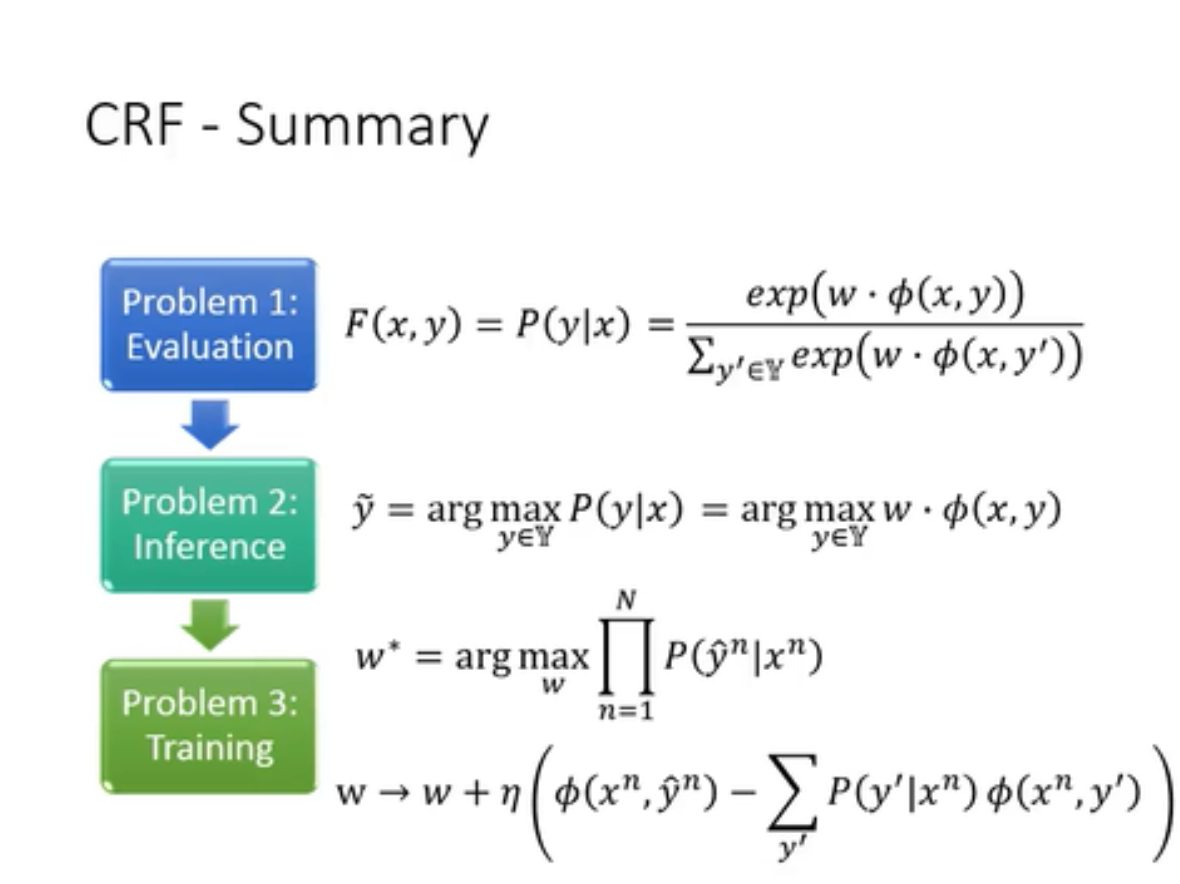
CRF vs HMM
本质区别:CRF会通过调整参数,尽可能降低错误对的机率,而HMM不具备这个功能
在计算中,HMM依据的是准确的P的值,而CRF只是根据训练集数据一直在训练调整参数,fit data。使得正确的对机率上升,错误对机率下降。